Nội dung bài viết sau đây Danang.Plus sẽ tổng hợp đầy đủ công thức đạo hàm cơ bản, đạo hàm cao cấp, quy tắc đạo hàm, đạo hàm lượng giác, bảng công thức đạo hàm và nguyên hàm gửi đến bạ đọc, nhằm giúp các bạn dễ dàng ôn lại kiến thức toán học của mình và có thể giải toán nhanh hơn, chính xác hơn.

Đạo hàm là gì? Định nghĩa đạo hàm
Đạo hàm là một khái niệm cơ bản trong giải tích toán học, đạo hàm của một hàm số là một đại lượng diễn tả sự biến thiên của hàm tại một điểm nào đó.
Định nghĩa: Đạo hàm của hàm số y=f(x) được ký hiệu là y′(x0) hoặc f′(x0):
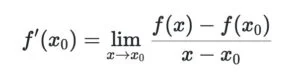
Hoặc:
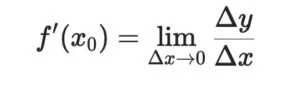
Trong đó:
- Số gia của đối số là x = x – x0.
- Số gia của hàm số là y = y – y0
Quy tắc đạo hàm
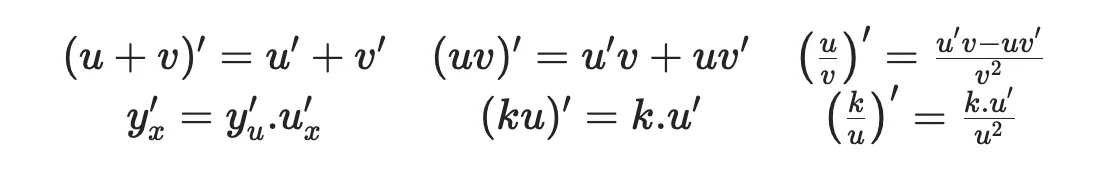
Đạo hàm các hàm số sơ cấp
Đạo hàm cấp cao
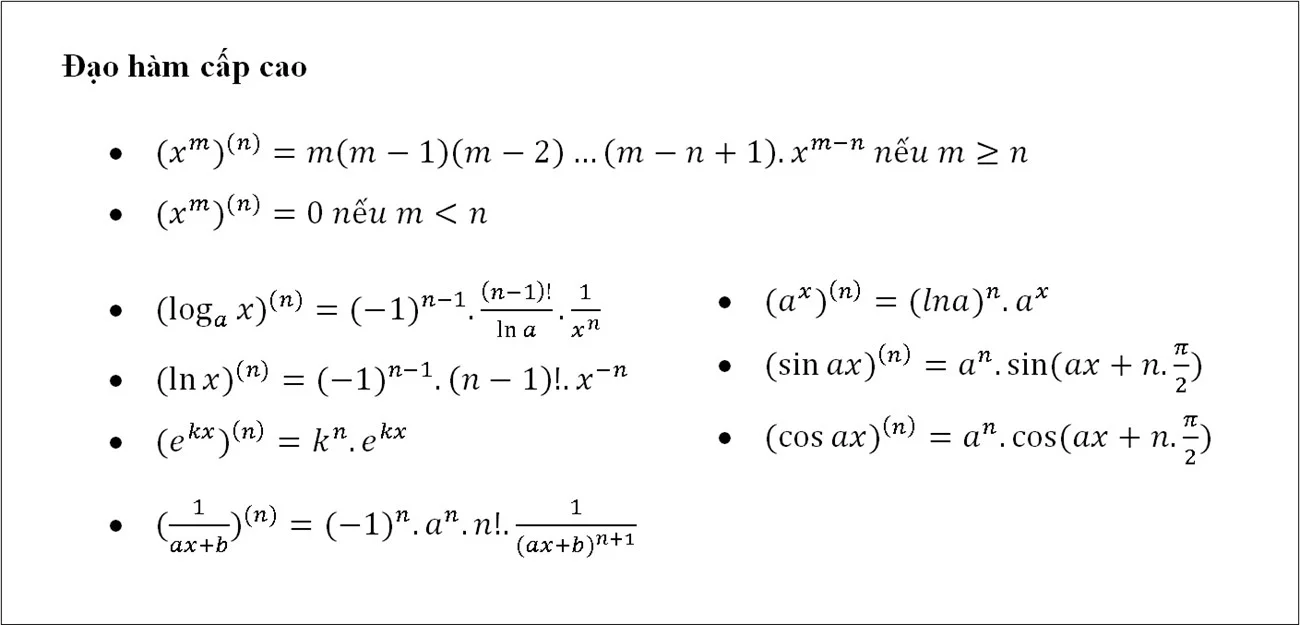
Công thức đạo hàm lượng giác
Dưới đây là bảng công thức đạo hàm lượng giác:

Bảng đạo hàm và nguyên hàm
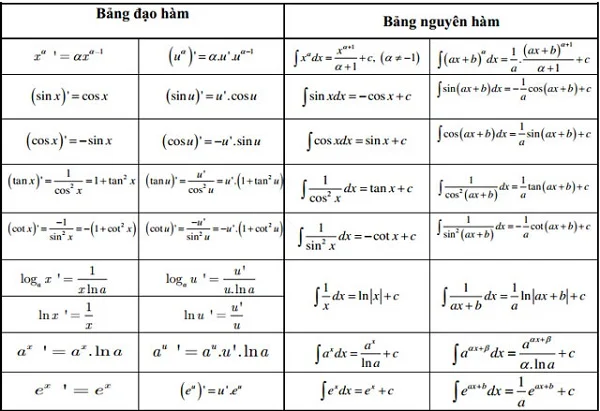
Một số bài tập Đạo hàm
Bài 1: Tìm đạo hàm của các hàm số sau:
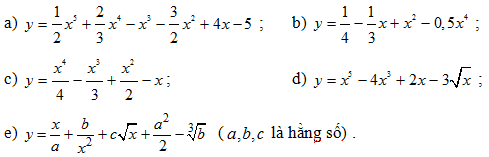
Đáp số:
a.
b.
c. y’ = x3 – x2 + x – 1
Bài 2: Tìm đạo hàm của các hàm số sau:
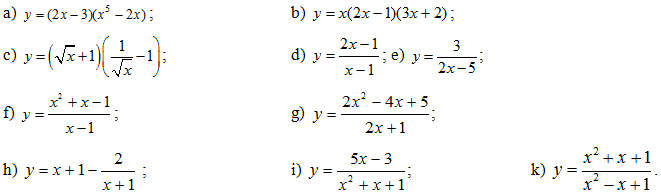
Đáp số:
| a. y’ = 12x5 – 8x -15x4 + 6 | b. y’ = 18x2 + 2x – 2 |
| c. |
d. y’ = -1/(x- 1)2 |
| e. y’ = -6/(2x – 5)2 | f. y’ = (x2 – 2x -1)/(x – 1)2 |
| g. y’=(8x3 – 8x2 + 4x – 10)/(2x + 1)2 | h. y’ = 1 + 2/(x + 1)2 |
| i. y’ = (-5x2 + 6x + 8)/(x2 + x + 1)2 | k. y’ = (-5x2 + 6x + 8)/(x2 – x + 1)2 |
Bài 3: Tìm đạo hàm của các hàm số sau:
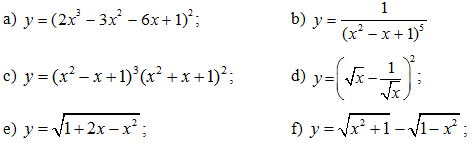
Bài 4: Cho hàm số ![]() . Xác định giá trị của tham số m để:
. Xác định giá trị của tham số m để:
a. y’ ≤ 0, ∀ x∈
b. y’ = 0 có hai nghiệm phân biệt cùng âm.
c. y’ = 0 có hai nghiệm phân biệt thỏa mãn điều kiện x12 + x22 = 3.
Bài 5: Cho hàm số (C): y = mx4 + (m2 – 9)x2 + 10 (1) (m là tham số). Xác định giá trị của m để hàm số có y’ = 0 có 3 nghiệm phân biệt.
Bài 6: Cho hàm số (C): y = x2 – 2x + 3. Viết phương trình tiếp tuyến với (C):
a. Tại điểm có hoành độ x0 = 2
b. Biết tiếp tuyến song song với đường thẳng 4x – y = 9
c. Vuông góc với đường thẳng 2x + 4y – 2011 = 0
d. Biết tiếp tuyến đi qua điểm A(1; 0)
Bài 7: Cho hàm số: ![]() (1).
(1).
a. Viết phương trình tiếp tuyến của (C) tại điểm M(-1;-1)
b. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
c. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
d. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng (d): 4x – y + 1 = 0
e. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (d’): 4x + y – 8 = 0
Hy vọng với những kiến thức tổng hợp về công thức đạo hàm mà Danang.Plus chia sẻ trong bài viết sẽ hữu ích với bạn đọc.









![Số taxi Đà Nẵng: Mai Linh, Vinasun, Tiên Sa, Sông Hàn,... [cập nhật 2022] 38 Số taxi Đà Nẵng](https://danang.plus/wp-content/uploads/2022/08/so-taxi-da-nang.jpg)